图形和Excel 图表(Excel charts)是可视化复杂数据集的好方法,贝尔(Bell)曲线也不例外。它们可以让您轻松分析正态分布,并且可以在Excel中轻松创建。让我们看看如何。
请记住,钟形曲线的目的不仅仅是美化数据。可以在此类图表上执行多种形式的数据分析,揭示数据集的许多趋势和特征。不过,在本指南中,我们将只专注于创建钟形曲线,而不是分析它。

正态分布(Normal Distribution)简介
钟形(Bell)曲线仅适用于可视化正态分布的数据集。因此,在深入研究钟形曲线之前,让我们先了解一下正态分布的含义。
基本上,任何值主要聚集在平均值周围的数据集都可以称为正态分布(或有时称为高斯分布)。大多数自然收集的数据集往往都是这样的,从员工绩效数据到每周销售数据。
什么是钟形曲线(Bell Curve)以及它为什么有用(Useful)?
由于正态分布的数据点聚集在均值周围,因此测量每个数据点相对于中心均值的方差比其绝对值更有用。以图表的形式绘制这些方差会产生钟形曲线(Bell Curve)。
这使您可以一目了然地发现异常值,并查看数据点相对于平均值的相对表现。对于员工评估和学生分数等事情,这使您能够区分表现不佳的人。
如何创建钟形曲线
与Excel 中的(simple charts in Excel)许多简单图表不同,您无法通过简单地在数据集上运行向导来创建钟形曲线。数据首先需要进行一些预处理。这是您需要做的:
- 首先按升序对数据进行排序。您可以通过选择整个列然后前往Data > Sort Ascending轻松完成此操作。

- 接下来,使用 Average 函数计算平均值(或 Mean) 。(calculate the average value (or Mean))由于结果通常为小数,因此最好将其与Round函数配对。
对于我们的示例数据集,该函数如下所示:
=ROUND(AVERAGE(D2:D11),0)

- 现在我们有两个用于计算标准差的(Standard Deviation)函数。当您只有总体样本(通常在统计研究中)时使用STDEV.S ,而当您拥有完整数据集时使用STDEV.P 。
对于大多数现实生活中的应用(员工评估、学生分数等),STDEV.P是(STDEV.P)理想的选择。您可以再次使用Round函数来获得整数。
=ROUND(STDEV.P(D2:D11),0)

- 所有这些只是为我们需要的实际值(正态分布)做准备工作(Normal)。当然,Excel也已经为此提供了专门的功能。
NORM.DIST函数接受四个参数 - 数据点、平均值、标准差和用于启用累积分布的布尔标志。(NORM.DIST)我们可以安全地忽略最后一个(输入FALSE),并且我们已经计算了平均值和偏差。这意味着我们只需要输入单元格值就可以得到结果。
=NORM.DIST(D2,$D$12,$D$13,FALSE)
对一个单元格执行此操作,然后将公式复制到整列- Excel将自动更改引用以匹配新位置。但请确保首先使用 $ 符号锁定平均值和标准差单元格引用。
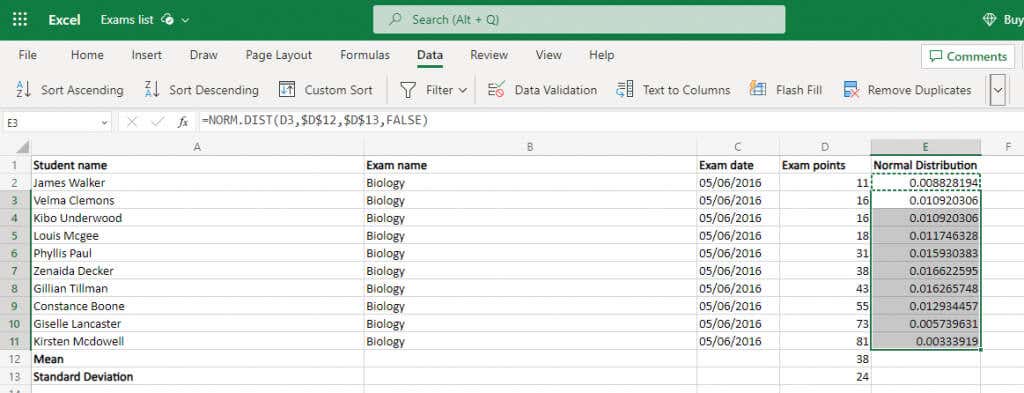
- 选择此正态分布以及原始值。分布将形成 y 轴,而原始数据点形成 x 轴。

- 前往“插入”(Insert)菜单并导航至散点图。选择“平滑线条(Smooth Lines)散布”(Scatter)选项。

在MS Excel中创建(MS Excel)钟形曲线图(Bell Curve Chart)的最佳方法是什么?
钟形(Bell)曲线图可能看起来很复杂,但实际上创建起来非常简单。您所需要的只是数据集的正态分布点。
首先,使用内置Excel公式确定平均值和标准差。然后使用这些值来计算整个数据集的正态分布。
钟形曲线图只是一个平滑线(Smooth Lines)散点图,使用 x 轴的原始数据点和 y 轴的正态分布值。如果您的数据集呈正态分布,您将在Excel中获得平滑的钟形曲线。
How to Create a Bell Curve Chart in Microsoft Excel
Grаphs and Excel charts are a great way to visualize complex datasets, and Bell curves are no exception. They let you analyze a normal distribution easily and can be easily created in Excel. Let’s find out how.
Keep in mind that the purpose of a bell curve goes beyond simply prettifying the data. There are many forms of data analysis that can be performed on such a chart, revealing many trends and characteristics of the dataset. For this guide, though, we will be only focusing on creating a bell curve, not analyzing it.

Introduction to a Normal Distribution
Bell curves are only useful to visualize datasets that are distributed normally. So before we dive into bell curves, let us take a look into what a normal distribution even means.
Basically, any dataset where the values are largely clustered around the mean can be called a normal distribution (or a Gaussian distribution as it is sometimes called). Most naturally collected datasets tend to be like that, from employee performance numbers to weekly sales figures.
What Is a Bell Curve And Why Is It Useful?
Since the data points of a normal distribution are clustered around the mean, it is more useful to measure the variance of each data point from the central mean rather than its absolute value. And plotting these variances in the form of a graph yields a Bell Curve.
This allows you to spot the outliers at a glance, as well as see the relative performance of the data points with respect to the average. For things like employee appraisals and student scores, this gives you the ability to tell the underperformers apart.
How to Create a Bell Curve
Unlike many simple charts in Excel, you cannot create a bell curve by simply running a wizard on your dataset. The data needs a bit of pre-processing first. Here is what you need to do:
- Begin by sorting the data in ascending order. You can do this easily by selecting the whole column and then heading to Data > Sort Ascending.

- Next, calculate the average value (or Mean) using the Average function. As the result is often in decimals, it is a good idea to pair it with the Round function as well.
For our sample dataset, the function looks something like this:
=ROUND(AVERAGE(D2:D11),0)

- Now we have two functions for calculating the Standard Deviation. STDEV.S is used when you only have a sample of the population (usually in statistical research) while STDEV.P is used when you have the complete dataset.
For most real-life applications (employee appraisal, student marks, etc.) the STDEV.P is ideal. Once again, you can use the Round function to get a whole number.
=ROUND(STDEV.P(D2:D11),0)

- All of this was just prep work for the real values we need – the Normal distribution. Of course, Excel already has a dedicated function for that as well.
The NORM.DIST function takes in four arguments – the data point, the mean, the standard deviation, and a boolean flag to enable cumulative distribution. We can safely ignore the last one (putting in FALSE) and we already calculated the mean and the deviation. This means we just need to feed in the cell values and we will get the result.
=NORM.DIST(D2,$D$12,$D$13,FALSE)
Do it for one cell and then just copy the formula over to the whole column – Excel will automatically change the references to match the new locations. But make sure to lock the mean and standard deviation cell references first by using a $ symbol.

- Select this normal distribution along with the original values. The distribution will form the y-axis while the original data points form the x-axis.

- Head to the Insert menu and navigate to the scatter diagrams. Select the Scatter with Smooth Lines option.

What Is the Best Way of Creating a Bell Curve Chart in MS Excel?
Bell curve charts might seem complicated, but are actually pretty simple to create. All you need is the normal distribution points of your dataset.
First, determine the mean and the standard deviation using built-in Excel formulas. Then use these values to calculate the normal distribution of the entire dataset.
The bell curve chart is just a Scatter with Smooth Lines plot using the original data points for the x-axis and the normal distribution values for the y-axis. If your dataset was normally distributed, you will get a smooth bell curve in Excel.







